Question

What is the value of each region that makes the inequalities true 5- 2x < -3-3(-5+ x) > 3

Answer 1

Let us solve for x in each of the inequalities.

The first inequality.

`5-2x<-3_{}`

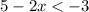
subtracting 5 from both sides gives

`5-2x-5<-3_{}-5`
`-2x<-8`

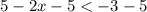
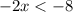
finally, multiplying both sides by -2 reverse the direction of the inequality to give

`-(2x)/(-2)>-(8)/(-2)`
`\boxed{x>4}`

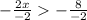
which is our answer!

The second inequality

`-3\mleft(-5+x\mright)>3`

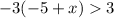
Dividing both sides by -3 gives

`(3(-5+x))/(-3)<(3)/(-3)`
`\rightarrow(-5+x)<-1`

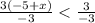
finally, adding -5 to both sides gives

`-5+x+5<-1+5`
`\begin{gathered} \rightarrow x<-1+5 \\ \boxed{x<4} \end{gathered}`

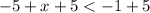
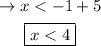
which is our answer!