Question

Graph the points and state whether they are collinear.(1,3), (0,2), (-4,0)Use the graphing tool to plot the given points.Click toenlargegraph

Answer 1

the points are not collinear

Step-by-step explanation

Step 1

Let

A(1,3)

B(0,2)

C(-4,0)

to know if the segments AB and BA are collinear, they must have the same slope if they are

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{where} \\ P1(x_1,y_1) \\ P2(x_2,y_2) \\ \end{gathered}`

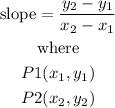
for segment AB

let

P1=A(1,3)

P2=B(0,2)

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ slope_(AB)=(2-3)/(0-1)=(-1)/(-1)=1 \\ slope_(AB)=1 \end{gathered}`

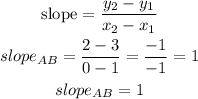
Step 2

for segment BC

P1=B(0,2)

P2=C(-4,0)

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(0-2)/(-4-0)=(-2)/(-4)=(1)/(2) \end{gathered}`

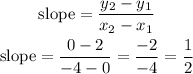
Step 3

compare the slopes

`\text{slope}_(AB)\\e slope_(BC)`

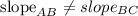
then, the points are not collinear