Question

F(x)=x^7-x^4 identify the zeros

Answer 1

x = 0 and x = 1

Step-by-step explanation

In the given function

`f(x)=x^7-x^4`

We can see clearly that one of the zeros is x = 0. Note that x is in all the terms of the polynomial, so whenever x is zero, the value of the function is zero.

According to the degree of this polynomial we should find 7 zeros. However, as we can see there are only two terms in this function and they all have x. Therefore, it is likely that the some of the zeros have a multiplicity greater than 1.

For x = 0, if we take x⁴ as a common factor:

`f(x)=x^4(x^3-1)`

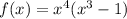
We can see that the multiplicity of this zero is 4.

Another zero is found by solving:

`x^3-1=0`

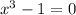
Add 1 to both sides of the equation:

`\begin{gathered} x^3-1+1=0+1 \\ x^3=1 \end{gathered}`

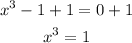
And take cubic root:

`\begin{gathered} \sqrt[3]{x^3}=\sqrt[3]{1} \\ x=1 \end{gathered}`

The other zero is x = 1, with multiplicity 3.

Since 4+3=7, we have found all the zeros of this function.