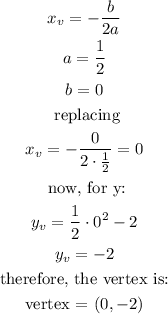Question

Hello, I really need help! Take a look at the picture. Thanks

Answer 1

`\begin{gathered} g(x)=(1)/(2)x^2-2 \\ \text{vertex = }(0,-2) \end{gathered}`

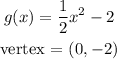
Explanation:

The first thing is to calculate step by step the transformations applied to the function f (x):

1. A vertical shrink

Is the compression of the graph towards the x-axis.

if 0 2. The reflection

If the function f (x) is reflected in the x-axis, then its image is g (x) = f (x)

3. Vertical translation

If the function f (x) is translated vertically down in n units, then your image would be:

g (x) = f (x) - n

Now, we apply this and the function would be:

`g(x)=(1)/(2)x^2-2`

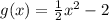
We can calculate the vertex as follows:

`\begin{gathered} x_v=-(b)/(2a) \\ a=(1)/(2) \\ b=0 \\ \text{ replacing} \\ x_v=-(0)/(2\cdot(1)/(2))=0 \\ \text{ now, for y:} \\ y_v=(1)/(2)\cdot0^2-2 \\ y_v=-2 \\ \text{therefore, the vertex is:} \\ \text{vertex = }(0,-2) \end{gathered}`