Question

Based on these sets of side lengths, which triangles are right triangles?O 8 units, 15 units, √75 unitsO 8 units, 3 units, √73 unitsO 16 units, 30 units, √50 unitsO 5 units, 7 units, √74 units

Answer 1

We will use the Pythagorean Theorem to check if the side lengths represent a right triangle.

The Pythagorean Theorem is given to be:

`c^2=a^2+b^2`

where c is the longest side length (the hypotenuse).

FIRST OPTION: 8 units, 15 units, √75 units

The longest side is 15 units. Therefore, we can check as follows:

`\begin{gathered} 15^2=8^2+(√(75))^2 \\ 225=64+75 \\ 225139 \end{gathered}`

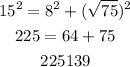
This is not a right triangle.

SECOND OPTION: 8 units, 3 units, √73 units

The longest side is √73 units. Therefore, we can check as follows:

`\begin{gathered} (√(73))^2=8^2+3^2 \\ 73=64+9 \\ 73=73 \end{gathered}`

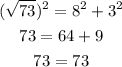
This is a right triangle.

Checking the remaining options in the same manner, the correct options are the SECOND and FOURTH OPTIONS.