Question

What is the minimum/ maximum value of the parabola and how was it determined? x^2+ 5x - 24 = 0

Answer 1

-30.25

Step-by-step explanation

The maximum or minimum value of a parabola is the y-coordinate of the vertex. If the parabola is given in the standard form,

`f(x)=ax^2+bx+c`

Then the x-coordinate of the vertex is,

`x_(vertex)=(-b)/(2a)`

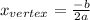
And the y-coordinate of the vertex is,

`y_(vertex)=f(x_(vertex))`

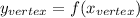
In this case, a = 1, and b = 5, so the x-coordinate of the vertex is,

`x_(vertex)=(-5)/(2\cdot1)=-(5)/(2)`

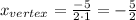
And the y-coordinate is,

`y_(vertex)=\left(-(5)/(2)\right)^2+5\left(-(5)/(2)\right)-24=(25)/(4)-(25)/(2)-24=(25-50-96)/(4)=(-121)/(4)=-30.25`

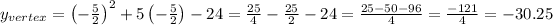
Hence, the minimum/maximum value of this parabola is -30.25.