the coordinates of the point three-fourths of the distance from A to B is (-1/4, 3 1/4)
See explanation below
Step-by-step explanation:
We will be using a problem on it to explain
Example: Find the coordinates of the point which is three fourth of the way from (2,1) t0 B(-1, 4)
There different method to approach such questions.
We will apply the formula below:
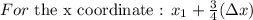
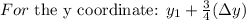
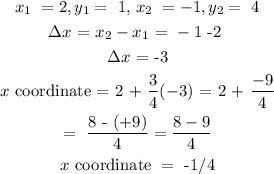
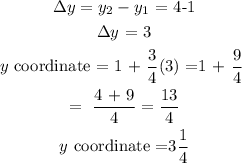
Hence, the coordinates of the point three-fourths of the distance from A to B is (-1/4, 3 1/4)