Question

Julio and jisel are selling pies for a fundraiser customers can buy cherry pies (x) and apple pies (y) julio sold 3 cherry pies and 14 apple pies for a total of $300. Jisel sold 3 cherry pies and 9 apple pies for a total of $210. Identify the equations that model the cost of the pies that Julio and jisel are selling. What is the cost for each cherry and apple pie ?

Answer 1

Let's represent the cherry pies and apple pies with variables

`\begin{gathered} \text{cherry pies=x} \\ \text{apple pies=y} \end{gathered}`

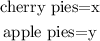
The equation of julio's sales will be

`\begin{gathered} 3* x+14* y=\text{ \$300} \\ 3x+14y=\text{ \$300 }\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots.(Eqn\text{ 1)} \end{gathered}`

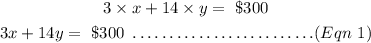
The equation of Jisel's sales will be

`\begin{gathered} 3* x+9* y=\text{ \$210} \\ 3x+9y=\text{ \$210}\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots..(Eqn\text{ 2)} \end{gathered}`

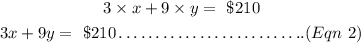
Let's combine Equations (1 )and (2 )and solve them simultaneously

`\begin{gathered} 3x+14y=\text{ \$300}\ldots\ldots\ldots\ldots\ldots\text{.}(\text{Eqn 1)} \\ 3x+9y=\text{ \$210}\ldots\ldots\ldots\ldots\ldots.(Eqn\text{ 2)} \end{gathered}`

Subtract Eqn (2) from Eqn (1) we will have

`\begin{gathered} 3x+14y-(3x+9y)=\text{ \$300- \$210} \\ 3x+14y-3x-9y=\text{ \$90} \\ 3x-3x+14y-9y\text{ =\$90} \\ 5y=\text{ \$90} \\ (5y)/(5)=\text{ }(90)/(5) \\ y=\text{ \$18} \end{gathered}`

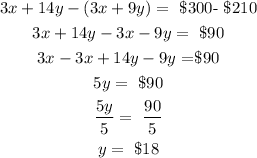
Substitute y= $18 in Eqn 1 we will have

`\begin{gathered} 3x+14y=\text{ \$300} \\ 3x+14(\text{ \$18)= \$300} \\ 3x+\text{ \$252= \$300} \\ 3x=\text{ \$300- \$252} \\ 3x=\text{ \$48} \\ (3x)/(3)=(48)/(3) \\ x=\text{ \$16} \end{gathered}`

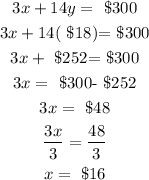
Therefore,

The equation for Julio's sales is 3x+14y= $300

The equation for Jisel's sales is 3x+9y= $210

The cost of one cherry pie is x= $16

The cost of one apple pie is y= $18