Question

The weights of gala apples follow a Normal distribution with a mean of 140 grams and a standard deviation of 12 grams. The owner of an apple orchard randomly selects 5 apples from the harvest and records the mean weight. What is the shape of the distribution of the sample mean for all possible random samples of size 5 from this population?

Answer 1

The shape is approximately normal, with mean of 140 grams and standard deviation of 5.37 grams.

Explanation:

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
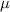`\mu` and standard deviation
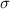`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
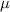`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

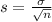For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
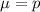`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

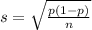
What is the shape of the distribution of the sample mean for all possible random samples of size 5 from this population?

By the Central Limit Theorem, the shape is approximately normal.

Mean is
`\mu = 140`

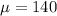
Standard deviation is
`s = (12)/(√(5)) = 5.37`

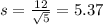
The shape is approximately normal, with mean of 140 grams and standard deviation of 5.37 grams.