Question

What are the solutions of this quadratic equation?x² + 8x + 3 = 0OAOB.OCOD.= 4 + √13= 8 + 2√13= -8 ± 2√13=-4 ± √13

Answer 1

The given quadratic equation is

x^2 + 8x + 3 = 0

The general form of a quadratic equation is expressed as

ax^2 + bx + c = 0

By comparing both equations,

a = 1

b = 8

c = 3

We would solve it by applying the formula for quadratic equations which is expressed as

`\begin{gathered} x\text{ = }\frac{-\text{ b}\pm√(b^2-4ac)}{2a} \\ Substitute\text{ the values. We have} \\ x\text{ = }\frac{-\text{ 8 }\pm√(8^2-4(1*3))}{2*1} \\ x\text{ = }\frac{-\text{ 8}\pm\sqrt{64\text{ - 12}}}{2} \\ x\text{ = }\frac{-\text{ 8 }\pm√(52)}{2} \\ x\text{ = }\frac{-\text{ 8}}{2}\pm(√(52))/(2) \end{gathered}`

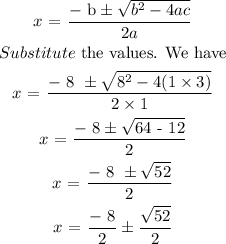
√52 can be written as 2√13

Thus,

x = - 4 ± 2√13/2

x = - 4 ± √13