Question

An early major objection to the idea that Earth is spinning on its axis was that Earth would turn so fast at the equator that people would be thrown off into space. What centripetal force is needed for a person of mass 57.3 kilograms at the equator? The radius of Earth is about 6450 kilometers.

Answer 1

1.954 N

Step-by-step explanation

Step 1

Diagram:

Step 2

to avoid the people thrown off into space the centripetal force has to be greater than his weight. Thus, we have to calculate the magnitudes of this forces:

so

`\begin{gathered} F_c=ma_c \\ W=mg \end{gathered}`

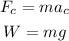
the centripetal acceleration is given by:

`a_c=(v^2)/(r)`

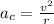
let, radius= 6450000 meters

Period = 24 hours= 24*3600 s= 86400 s

and

`\begin{gathered} v=(distancetraveled)/(T(period))=(2\pi r)/(T) \\ v=\frac{2*\pi *6450000m}{24*3600\text{ s}}=(40526.54)/(86400)=469.057\text{ }(m)/(s) \end{gathered}`

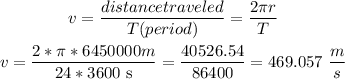
Step 2

a)find the centripetal force:

`\begin{gathered} F_(c)=ma_(c) \\ F_c=m(v^2)/(r) \\ F_c=57.3\text{ Kg}\frac{(469.057(m)/(s))^2}{6450000\text{ m}} \\ F_c=1.954\text{ N} \end{gathered}`

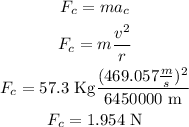
b) finally we can conclude

The centripetal force needed is 1.954 N