Question

A cone and a cylinder have equal radius, r, and equal altitudes, h. If the slant height of the cone is l, then the ratio of the lateral area of the cone to the lateral area of the cylinder isA. l:2rB. l:2hC. 2l:hD. l:h

Answer 1

Given:

radius of cone = r

height of cone = h

radius of cylinder = r

height of cylinder = h

slant height of cone = l

Solution

The lateral area (A) of a cone can be found using the formula:

`A\text{ = }\pi rl`

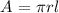
where r is the radius and l is the slant height

The lateral area (A) of a cylinder can be found using the formula:

`A\text{ = 2}\pi rh`

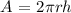
The ratio of the lateral area of the cone to the lateral area of the cylinder is:

`\pi rl\text{ : 2}\pi rh`

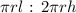
Canceling out, we have:

`\begin{gathered} =(\pi rl)/(2\pi rh) \\ =\text{ }(l)/(2h)\text{ or l:2h} \end{gathered}`

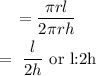
Hence the Answer is option B