Question

Need to figure out the domain and range in interval notation and the asymptote

Answer 1

Given:

`y=e^(-x)-2`

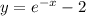
The domain of a function is the set of input values that make the function defined.

Hence, for the function given, there are no undefined points for the function.

`The\text{ domain is }-\infty<p></p><p><strong>Thus, the domain in interval notation is</strong>:</p>[tex]\begin{gathered} \\ (-\infty,\infty) \end{gathered}`

The range of a function is the set of output values that make the function defined.

The range of the exponential function is given by:

`y>-2`

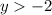
Therefore, in interval notation, the range is:

`(-2,\infty)`

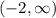
The asymptote is a line that a graph approaches without touching it.

The graph of the function is shown:

Hence, it has a horizontal asymptote as the curve bends towards the horizontal line at y = -2.

Therefore, the asymptote exists at y = -2