Solution:
To find the percentage of American women who have shoe sizes that are greater than 11.11, we apply the z score formula first
The z score formula is
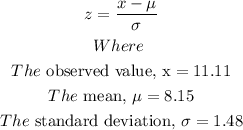
Substitute the variables into the formula above
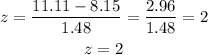
Given that the z = 2
From the deduction above, the given value is 2 standard deviation away to the right of the mean.
According to the empirical rule,
Using the chart below
The percentage of American women who have shoe sizes that are greater than 11.11 is
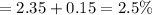
Hence, the answer is 2.5%