ANSWER
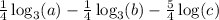
Step-by-step explanation
First we can take the root out of the argument of the logarithm. Remember that roots can be written as fractional exponents:
![\sqrt[4]{(a)/(bc^5)}=\mleft((a)/(bc^5)\mright)^(1/4)](https://img.qammunity.org/2023/formulas/mathematics/college/2utfi948yinhue53zohw1ju65hnda0379g.png)
So applying the power rule of logarithms:
![\log _3\sqrt[4]{(a)/(bc^5)}=(1)/(4)\log _3(a)/(bc^5)](https://img.qammunity.org/2023/formulas/mathematics/college/76d38x1d5b0j86xuoecxr6bwq3hzcjc7bj.png)
Next we can apply the quotient rule of logarithms:

Then we use the product rule for the last term:
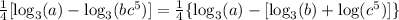
And the power rule for the exponent of c:

What we have to do now is rewrite this to be more clear. Apply the distributive property for the minus sign into the expression with the logarithms of b and c:
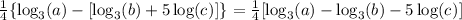
And then do the same for the 1/4 coefficient:
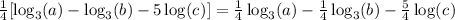
In summary:
![\log _3\sqrt[4]{(a)/(bc^5)}=(1)/(4)\log _3(a)-(1)/(4)\log _3(b)-(5)/(4)\log (c^{})](https://img.qammunity.org/2023/formulas/mathematics/college/s7md41h21jf6gshd1fwkwe8cgsnglkjhul.png)