The formula to calculate the midpoint between two points is,
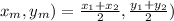
Checking the last option for confirmation
The coordinates are (10, 0) and (6, 6)
Where,
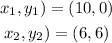
Therefore,
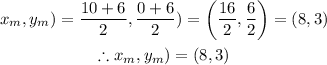
Hence, from the result above we can conclude that the coordinates with the pair (8,3) are (10, 0) and (6, 6).
Therefore, the answer is (10, 0) and (6, 6).