The expression 4^2/3 can be written in a radical form as:
![\sqrt[3]{4^2}](https://img.qammunity.org/2023/formulas/mathematics/college/126qtulei9ucnnmmbhwrd5lfkpddk52wp0.png)
in which if we apply the exponent to its base 4, the equation will become:
![\sqrt[3]{16}](https://img.qammunity.org/2023/formulas/mathematics/high-school/39opq144jsu8kqrlhs3mtwtgcj20nr1yn8.png)
So, Option 3 is equivalent to the expression.
Let's take a look at other expressions.
![(\sqrt[3]{4})^2\Rightarrow(4^{(1)/(3)})^2\Rightarrow4^{(2)/(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/zgv50wiztf6fxdvb9amq0wey0a01wyj38z.png)
Option 4 is also equivalent to the expression.
For Option 2,
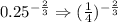
To make the exponent positive, we take the reciprocal of 1/4 and that is 4. Hence,
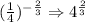
Option 2 is also equivalent to the given expression.
Therefore, the expression that is NOT equivalent to 4^2/3 is Option 1.