Recall the inverse proportionality relationship: If m is inversely proportional to n, then the relationship is:
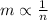
Substitute y and √x for m and n respectively in the relationship:
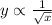
Applying a constant of proportionality, k, the relationship becomes:
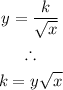
The question gives the following values for x and y:
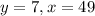
Substituting these into the equation for k, the value of k can be gotten to be:
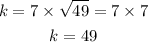
The constant of proportionality is 49.
The correct answer is FALSE.