Question

Eight percent of all college graduates hired by companies stay with the same company for more than five years. The probability, rounded to four decimal places, that in a random sample of 11 such college graduates hired recently by companies, exactly 2 will stay with the same company for more than five years is: the absolute tolerance is /-0.0001

Answer 1

0.1662 = 16.62% probability that exactly 2 will stay with the same company for more than five years

Explanation:

For each graduate, there are only two possible outcomes. Either they stay for the same company for more than five years, or they do not. Graduates are independent. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

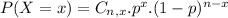
In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

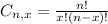
And p is the probability of X happening.

Eight percent of all college graduates hired by companies stay with the same company for more than five years.

This means that
`p = 0.08`

Sample of 11 college graduates:

This means that
`n = 11`

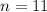
The probability, rounded to four decimal places, that in a random sample of 11 such college graduates hired recently by companies, exactly 2 will stay with the same company for more than five years is: the absolute tolerance is +-0.0001

The tolerance means that the answer is rounded to four decimal places.

The probability is P(X = 2). So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(11,2).(0.08)^(2).(0.92)^(11) = 0.1662`

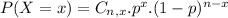
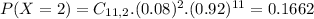
0.1662 = 16.62% probability that exactly 2 will stay with the same company for more than five years