Answer:
pf = 198.8 kg*m/s
θ = 46.8º N of E.
Step-by-step explanation:
- Since total momentum is conserved, and momentum is a vector, the components of the momentum along two axes perpendicular each other must be conserved too.
- If we call the positive x- axis to the W-E direction, and the positive y-axis to the S-N direction, we can write the following equation for the initial momentum along the x-axis:
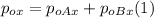
- We can do exactly the same for the initial momentum along the y-axis:
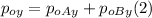
- The final momentum along the x-axis, since the collision is inelastic and both objects stick together after the collision, can be written as follows:
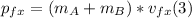
- We can repeat the process for the y-axis, as follows:
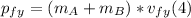
- Since (1) is equal to (3), replacing for the givens, and since p₀Bₓ = 0, we can solve for vfₓ as follows:
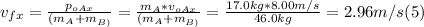
- In the same way, we can find the component of the final momentum along the y-axis, as follows:
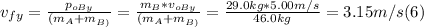
- With the values of vfx and vfy, we can find the magnitude of the final speed of the two-object system, applying the Pythagorean Theorem, as follows:
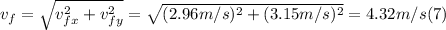
- The magnitude of the final total momentum is just the product of the combined mass of both objects times the magnitude of the final speed:
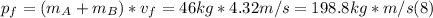
- Finally, the angle that the final momentum vector makes with the positive x-axis, is the same that the final velocity vector makes with it.
- We can find this angle applying the definition of tangent of an angle, as follows:
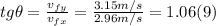
⇒ θ = tg⁻¹ (1.06) = 46.8º N of E