Step-by-step explanation
a) We rewrite the right side of the expression as:
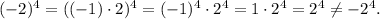
So we see that the expression of point a is FALSE.
b) We consider the expression:
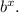
We take the logarithm in base b, we get:
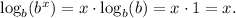
We see that the logarithm of a number x to a base b is just the exponent you put onto b to make the result equal x. We conclude that this expression is TRUE.
c) We know that in any base a, we have:
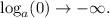
We conclude that the expression of this item is FALSE.
d) Logarithms are defined only for numbers greater than 0. So we conclude that this expression is FALSE.
e) We consider the expression:
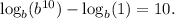
Applying the properties of logarithms, we get:

We see that this expression is TRUE.
Answer
a) FALSE
b) TRUE
c) FALSE
d) FALSE
e) TRUE