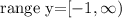The expressi
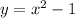
and we would like to know the domain and range of the function. Since for every x value we give to the equation the result will always be a real number the domain of this function is
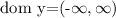
Now to find the range of the function we solve the equation for x.
![\begin{gathered} y=x^2-1 \\ x^2=y+1 \\ x=\pm\sqrt[]{y+1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6uotuvdbqt2xibwl4yiqccc7oxqq5tquht.png)
This root will only exist if
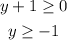
Therefore the range of the function is: