Let x be the missing side. Since we have a right triangle, we can apply Pythagorean theorem:
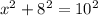
Remember that the hypotenuse (10 in our case) is always in front of the right angle. Then, from the last result, we have

By subtracting 64 to both sides, we get
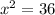
then x is given by
![\begin{gathered} x=\sqrt[]{36} \\ x=6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k1y0gmofqr37ykm22ob0jftrrudgo2i1iy.png)
Therefore, the answer is: 6