Events M and N are independent events.
It means that the outcome of one event does not affect the outcome of the other event.
The probability of events M and N both occurring is given by
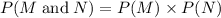
Re-arranging for P(N), we get
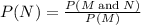
Where
P(M and N) = 0.158
P(M) = 0.23
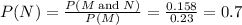
Therefore, the probability P(N) is 0.7