Question

I need help with this question I’m not sure where to even begin

Answer 1

We will have the following:

a. We determine the tension force of T2 as follows:

We know that the system must be at equilibrium on the horizontal axis:

`\sum F_x=T_1cos(42.5)+T_2cos(36.5)=0`

So:

`\begin{gathered} T_2cos(36.5)=-(1235N)cos(42.5)\Rightarrow T_2=-((1235N)cos(42.5))/(cos(36.5)) \\ \\ \Rightarrow T_2=1132.711003...N\Rightarrow T_2\approx1132.7N \end{gathered}`

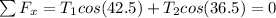
So, the value of T2 is approximately 1132.7 N.

b. We will determine the torques created by T1 and T2 as follows:

T1:

`\tau_(T1)=(10m)(1235N)sin(42.5)\Rightarrow\tau_(T1)\approx8343.5N\ast m`

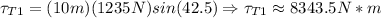
T2:

`\tau_(T2)=(10m)(1132.7N)sin(36.5)\Rightarrow\tau_(T2)\approx6737.6N\ast m`

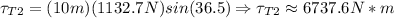
So the torques of T1 and T2 on the base are approximately 8343.5 N*m and 6737.6 N*m respectively.

c. The torques around that axis generated by the normal force and the weight are both 0 N*, since they are parallel to the axis.

d. We will determine the angular acceleration as follows:

`\begin{gathered} \alpha=(\tau_(T1))/(I)\Rightarrow\alpha=(\tau_(T1))/((1/3mL^2)) \\ \\ \Rightarrow\alpha=((8343.5N\ast m))/((1/3(200kg)(10m)^2))\Rightarrow\alpha=1.251525rad/s^2 \\ \\ \Rightarrow\alpha\approx1.25rad/s^2 \end{gathered}`

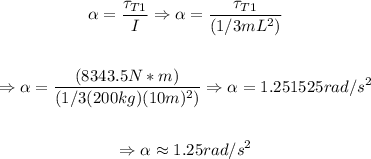
So, the angular acceleration is approximately 1.25 radians/ s^2.