Question

Value of x for 12(x-2)+3x=1/2(x+6)+2

Answer 1

Given

`12(x-2)+3x=(1)/(2)(x+6)+2`

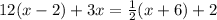
The objective is to determine the value of x

The first step is to distribute the multiplication in both parentheses terms

`\begin{gathered} (12\cdot x)-(12\cdot2)+3x=((1)/(2)\cdot x)+((1)/(2)\cdot6)+2 \\ 12x-24+3x=(1)/(2)x+3+2 \end{gathered}`

The second step, order the like terms and simplify them

`\begin{gathered} 12x+3x-24=(1)/(2)x+3+2 \\ 15x-24=(1)/(2)x+5 \end{gathered}`

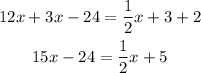
The third step is to pass the x-term to the left side of the equal sign and the constants to the right side. For this, you have to apply the opposite operation to both sides of it, this means you have to subtract 1/2x to both sides of the equation and add 24

`\begin{gathered} 15x-(1)/(2)x-24=(1)/(2)x-(1)/(2)x+5 \\ (29)/(2)x-24=5 \\ (29)/(2)x-24+24=5+24 \\ (29)/(2)x=29 \end{gathered}`

The final step is to cancel the multiplication on the x-term, for this you have to multiply the fraction by its reciprocal (inverse fraction), and to keep the equality valid, what is done in one side must be done to the other side, so multiply 29 by the reciprocal fraction too.

`\begin{gathered} ((2)/(29)\cdot(29)/(2))x=29\cdot(2)/(29) \\ x=2 \end{gathered}`

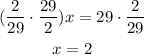
The value of x is 2