Question

the points R (-3,9),S(-9,3),T(-6,0) and U (0,6) form a quadrilateral. find the desired slopes and lengths, then fill in the words that best identifies the type of quadrilateral

Answer 1

• slope of RS = 1

,

• slope of ST = -1

,

• slope of TU = 1

• slope UR = -1

STEP - BY - STEP EXPLANATION

What to find?

• Slope of RS

,

• Slope of ST

,

• Slope of TU

,

• Slope of UR

The formula used in finding the slope between two points is given by;

`\text{slope(m)}=(y_2-y_1)/(x_2-x_1)`

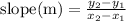
To find slope RS;

R (-3,9),S(-9,3)

x₁ = -3 y₁=9 x₂=-9 y₂=3

Substitute the values into the formula and simplify.

`\text{Slope RS=}(3-9)/(-9+3)=(-6)/(-6)=1`

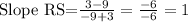
Hence, slope RS = 1

Slope ST

S(-9,3),T(-6,0)

x₁ = -9 y₁=3 x₂=-6 y₂=0

Substitute the values into the formula and simplify.

`\text{Slope ST=}(0-3)/(-6+9)=(-3)/(3)=-1`

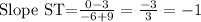
Hence, slope ST = -1

Slope TU

T(-6,0) , U (0,6)

x₁ = -6 y₁=0 x₂=0 y₂=6

Substitute the values into the formula and simplify.

`\text{Slope TU=}(6-0)/(0+6)=(6)/(6)=1`

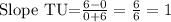
Hence, slope TU = 1

Slope UR

U (0,6), R (-3,9)

x₁ = 0 y₁=6 x₂=-3 y₂=9

Substitute the values into the formula and simplify.

`\text{Slope UR=}(9-6)/(-3-0)=(3)/(-3)=-1`

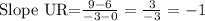
Hence, slope UR = -1