Answer:
14 cm
Step-by-step explanation:
The area of a square is calculated as
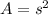
Where s is the length of its side. Since the area is 98 cm², the length of the side is equal to
![\begin{gathered} 98=s^2 \\ \sqrt[]{98}=s \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k1xgdi5oyveftiu8h2eexror5z1j28gks7.png)
Now, the length of the diagonal can be calculated using the Pythagorean theorem where the legs are √98 and the hypotenuse is the diagonal, so
![\begin{gathered} d=\sqrt[]{(\sqrt[]{98})^2+(\sqrt[]{98})^2} \\ d=\sqrt[]{98+98} \\ d=196 \\ d=14 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ue5lwu32zdk9pbpkicfrajq0bfq6net28n.png)
Therefore, the length of its diagonal is 14 cm