Before we can determine the rectangular coordinate of the point, let's determine first its polar coordinates. For this, we need two things: radius and angle.
For the radius, we see that point R is 4 units away from the center.
For the angle, we see that it is 30° clockwise or 330° counterclockwise. See the illustration below:
Now that we know the radius is 4 units and the angle is 330° counterclockwise, let's now convert this to rectangular coordinates.
Use the formula below:
For x-coordinate, we have:
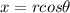
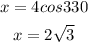
For the y-coordinate, we have:
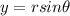
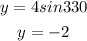
Therefore, the rectangular coordinate of the given polar point is (2√3, -2). Option B.