Question

An instructor wishes to determine the wavelength of the light in a laser beam. To do so, she directs the beam toward a partition with two tiny slits separated by 0.180 mm. An interference pattern appears on a screen that lies 5.30 m from the slit pair. The instructor's measurements show that two adjacent bright interference fringes lie 1.60 cm apart on the screen. What is the laser's wavelength (in nm) ?

Answer 1

λ = 5.434 x 10⁻⁷ m = 543.4 nm

Step-by-step explanation:

To solve this problem we can use the formula provided by Young's Double Slit experiment:

`\Delta x = (\lambda L)/(d)\\\\\lambda = (\Delta xd)/(L)`

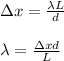
where,

λ = wavelength of light = ?

Δx = distance between adjacent bright fringes = 1.6 cm = 0.016 m

d = slit separation = 0.18 mm = 0.00018 m

L = Distance between slits and screen = 5.3 m

Therefore,

`\lambda = ((0.016\ m)(0.00018\ m))/(5.3\ m)`

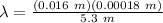
λ = 5.434 x 10⁻⁷ m = 543.4 nm