Question

The sum of the digits of the area7 m12 m2 m9 m22 m

Answer 1

Let's begin by dividing the figure into shapes we can more easily calculate the area of:

We have divided the figure into rectangles 1, 2 and 3. Le'ts first observe that the base of rectangle 2 will measure 3m, since 22-7-12=3. Likewise, its height will measure 7m since 9-2=7.

From here, we can calculate the area of each rectangle using the formula

`A=b\cdot h`

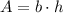
where b is the lenght of the base and h is the lenght of the height. Using this formua on each rectangle we get:

`A_1=7\cdot9=63`
`A_2=3\cdot7=21`
`A_3=9\cdot12=108`

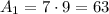
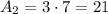
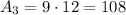
Knowing this, the area of the whole figure will be

`A_T=A_1+A_2+A_3=63+21+108=192`

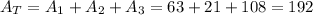
Finally, we sum the digits of this area:

`1+9+2=12`

So the answer is 12m.