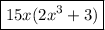In this problem, we want to complete factor a given expression:
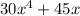
We will begin by finding the greatest common factor for the two terms. Let's begin with 30 and 45.
The Greatest Common Factor of 30 and 45 is:
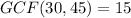
Then, we find the greatest common factor of x⁴ and x:
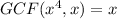
So the greatest common factor of both terms is:
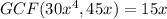
When we factor this, it means we are dividing the greatest common factor from the two terms to pull it out of the expression.
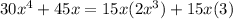
We can pull the 15x outside a group of parentheses to get: