Answer:
![\frac{33+11\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/82kqsqa3awqcs2gnzvlydqebwrmuxls213.png)
Step-by-step explanation:
The 30/60/90 triangle is given below
The perimeter of the triangle is

therefore, we need to find the value of x and y.
The value of x is given by
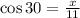
multiplying both sides by 11 gives

now
![\cos 30=\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/4ebiugiygusoldhkp1taritnl4s5heakjf.png)
therefore.
![\boxed{x=11\cdot\frac{\sqrt[]{3}}{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/fm5raf9zt4w5nuzq6ykdt8a8lf7jw1oudi.png)
Now we fidn the value of y.
The value of y is given by

multiplying both sides by 11 gives
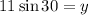
Now since
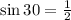
we have
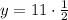

with the value of x and y in hand, wecan now find the perimeter.
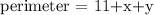
![perimeter=11+(11)/(2)+\frac{11\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/r5usezardl81fifyxrosllymwzmxn51vnf.png)
which simplifies to give
![perimeter=\frac{33+11\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/gso0hs7vwbbomleobmqnx8dnu8idgfa79p.png)
which is our answer!