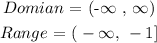Step 1:
Write the function
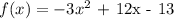
a)
To find the y-intercept, plug x = 0 and to find the x-intercept, plug y = 0

b) To graph the function, you will need to find the vertex, the global maximum.
The extreme point is ( 2 , -1 )
Global maximum = ( 2 , -1 )
So you can graph the function using y-intercept (0, -13) and the global maximum (2 , -1)
c)
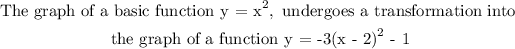
The graph undergoes the following transformation
1. stretched by a factor of 3
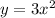
2. Then reflect over the x-axis
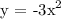
3. Then shift to the right by a factor of 2 units
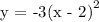
4. The finally shift vertically downward by 1 unit

d)
e)