Question

Two objects are initially at the x = 0 meter mark at t=0 seconds. Object #1 has an initial velocity of 9.00 m/s i and undergoes a constant acceleration of 3.00 m/s2 i. Object #2 is initially at rest and undergoes a constant acceleration of 5.00 m/s2 i. a) What is the distance between the objects at t=4.00 seconds b) What is the distance between the objects when they have the same velocity?

Answer 1

a) We will determine the distance traveled by each object first, that is:

Object 1:

`d_1=(9m/s)(4s)+(1)/(2)(3m/s^2)(4s)^2\Rightarrow d_1=60m`

Object 2:

`d_2=(0m/s)(4s)+(1)/(2)(5m/s^2)(4s)^2\Rightarrow d_2=40m`

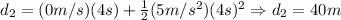
So, both objects are 20 meters apart after 4 seconds.

b) Now, we determine the distance when they have the same velocity, that is:

First, we determine the time it takes for them to have the same velocity:

`(1)/(2)(5m/s^2)t^2=(9m/s)t+(1)/(2)(3m/s^2)t^2\Rightarrow(1m/s^2)t^2-(9m/s)t=0`
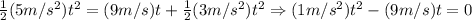
`\Rightarrow t=\frac{-(-9)\pm\sqrt[]{(-9)^2-4(1)(0)}}{2(1)}\Rightarrow\begin{cases}t=9s \\ \\ t=0s\end{cases}`

So, after 9 seconds they will have the same velocity, now we determine the distance between them:

Object 1:

`d_1=(9m/s)(9s)+(1)/(2)(3m/s^2)(9s)^2\Rightarrow d_1=202.5m`

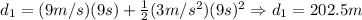
Object 2:

`d_2=(0m/s)(9s)+(1)/(2)(5m/s^2)(9s)^2\Rightarrow d_2=202.5m`

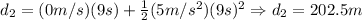
The distance between the two objects when they have the same velocity is 0 meters. They are in the same place.