Answer:
(x + 3)*(x + 1.5)
Explanation:
Factoring a second degree polynomial:
Suppose we have a second degree polynomial in the following format:
ax² + bx + c = 0
It's factorization is given by:
a(x - x')(x - x'')
In which x' and x'' are the roots of the polynomial.
Finding the roots of a polynomial:
The roots of the polynomial above are given by:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this question:
The polynomial is: 2x² + 9x + 9
So a = 2, b = 9, c = 9.
The roots are:
![x=\frac{-9\pm\sqrt[]{9^2-4\ast2\ast9}}{2\ast2}=(-9\pm3)/(4)](https://img.qammunity.org/2023/formulas/mathematics/college/drovpek70ii711fgey4d2hqfk1uwuq0u1p.png)
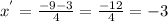
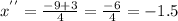
So, the factorization is:
(x - (-3))*(x - (-1.5)) = (x + 3)*(x + 1.5)