Question

Find features such as x and y intercepts to sketch this function (using e or in is not allowed)

Answer 1

Let's find the x-intercept of the given function. This ocurrs when y is equal to zero, so we have

`0=-log_2(3(x+2))+4`

which gives

`4-log_2(3(x+2))=0`

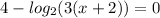
Now, we can rewrite the number 4 as follows

`4=log_22^4`

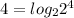
So, by substituting this result into the above equation, we have

`log_22^4-log_2(3(x+2))=0`

From the quotient rule of the logarithms, it can be written as

`log_2(2^4)/(3(x+2))=0`

From the property

`log_b1=0`

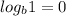
we can conclude that

`(2^4)/(3(x+2))=1`

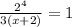
or equivalently,

`(16)/(3(x+2))=1`

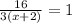
so, we have

`3(x+2)=16`

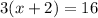
which gives

`\begin{gathered} x+2=(16)/(3) \\ then \\ x=(16)/(3)+2=7.3333 \end{gathered}`

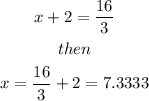
So, we have obtained that the x-intercept is the point (7.333, 0).

Similarly, the y-intercept ocurrs at x=0, which implies that

`y=-log_2(3(0+2))+4`

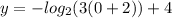
or equivalently,

`y=-log_2(-6)+4`

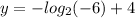
However, for a real base (2 in our case) the logarithm is undefined. This fact and since the logarithm has negative coefficient mean that the graph of the function has the form:

As we can corroborate with the followin graph: