Question

Erica claims if a cylinder has an equal radius and height , and its surface area it 64pie square inches, what is its volume?

Answer 1

From the question,the radius and the height are equal, Hence

`\begin{gathered} r=h \\ surfaceArea=64\pi in^2 \end{gathered}`

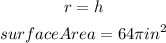
The formula for surface area is

`\begin{gathered} \text{Surface Area=2}\pi r^2+2\pi rh \\ \end{gathered}`

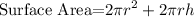
Since

`\begin{gathered} r=h \\ \text{Surface Area=2}\pi r^2+2\pi r(r)=2\pi r^2+2\pi r^2=4\pi r^2 \\ \text{Hence } \\ \text{surface Area=4}\pi r^2 \end{gathered}`

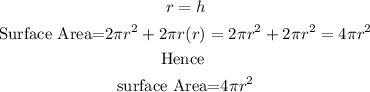
Equate the formula to the surface Area to find the value of r

`\begin{gathered} \text{surface Area=4}\pi r^2 \\ 64\pi=4\pi r^2 \\ \text{divide both sides by 4}\pi,\text{ we have } \\ (64\pi)/(4\pi)=(4\pi r^2)/(4\pi) \\ 16=r^2 \\ \text{taking square root of both sides, } \\ r=\sqrt[]{16} \\ r=4in \end{gathered}`

hence

r= 4 inches

Then the volume of the cylinder will be;

`\begin{gathered} \text{volume = }\pi r^2h \\ \text{Where r=h=4} \end{gathered}`

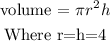
Substitute the value of r, we have

`\begin{gathered} \text{Volume}=\pi4^2(4) \\ \text{volume}=64\pi in^3 \end{gathered}`

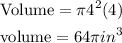
Hence

The volume of the cylinder will be 64π in³