Question

Suppose the mean' height in inches of all 9th grade students at one high school isestimated. The population standard deviation is 5 inches. The heights of 7randomly selected students are 60, 75, 69, 72, 61, 74 and 64= Ex: 12.34Margin of error at 95% confidence level = Ex: 1.23=95% confidence interval = [ Ex: 12.34 Ex: 12.34 ][smaller value larger valuel

Answer 1

- Calculate the sample mean x:

`\bar{x}=(60+75+69+72+61+74+64)/(7)=(475)/(7)=67.86`

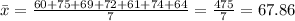
The population standard deviation is 5 inches.

Confidence level is 95% = 0.95

Therefore, the significance level is 1 - 0.95 = 0.05

- So, using standard normal table, the one sided critical value for 95% confidence level is 1.96. Then the margin of error is given by:

`\begin{gathered} E=1.96*(\sigma)/(√(n)) \\ Where\text{ }\sigma=5\text{ and n}=7 \end{gathered}`

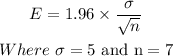
Substitute the values:

`E=1.96*(5)/(√(7))=3.7041`

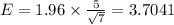
- The formula for confidence interval is given as:

`\begin{gathered} \bar{x}\pm1.96*(\sigma)/(√(n)) \\ or \\ \bar{x}\pm E \end{gathered}`

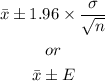
Therefore, the intervals are:

smaller value

`67.86-3.7041=64.16`

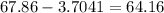
larger value

`67.86+3.7041=71.56`

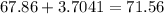
Answer:

`\bar{x}=67.86`

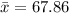
Margin of error at 95% confidence level = 3.70

95% confidence interval = [ 64.16, 71.56 ]