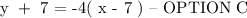Question

Which is the correct point slope form of the equation for the line that contains thepoints (4,5) and (7,-7)?

Answer 1

Step 1:

In this question, we are given the following:

The correct point-slope form of the equation for the line that contains the

points (4,5) and (7,-7).

Step 2:

`\begin{gathered} \text{The slope form of equation of the line : y - y}_1=m(x-x_1) \\ m\text{ = }(y_2-y_1)/(x_2-x_1) \\ \text{where ( x}_1,y_1)\text{ = ( 4, 5)} \\ (x_2,y_2)\text{ = ( 7, -7)} \\ m\text{ = }(-7-5)/(7-4)=(-12)/(3)=\text{ -4} \end{gathered}`

Step 3:

Using the formulae,

`\begin{gathered} y-y_1_{}=m(x-x_1)\text{ } \\ y\text{ -5 = - 4( x -4)} \\ y\text{ -5 = -4x + 16} \\ y\text{ + 4x = 16+ 5} \\ 4x\text{ + y = 21 which can be wr}itten\text{ as: y = -4 x + 21 which is also } \\ \text{y + 7 = - 4 ( x - 7 )} \\ \text{check:}=\text{ (4, 5 ) : 5+ 7 =-4(4-7) = 12 (correct)} \\ \text{check:}=(7,\text{ -7): -7+ 7 = -4(7-7) =0 )( correct)} \end{gathered}`

CONCLUSION:

The correct point-slope form of the equation for the line is:

`\text{y }+\text{ 7 = -4( x - 7 ) -- OPTION C}`