We have two integers (x and y).
The largest integer (y) is 3 more than 5 times the smallest integer (x).
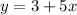
Also, the smaller (x) substracted from the larger (y) is 31.
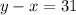
We can replace the value of y from the second equation in the first equation and solve:

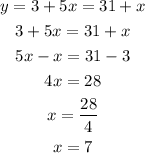
Then, the value of y is:
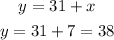
The integers are 7 and 38.