Question

Applying a force of 20 N to a 0.4 kg puck as it slides along to frictionless surface from rest to 10 ms-1 in 0.2 s. Calculate the work done by the puck.A. 2000 JB. 200 JC. 20 J

Answer 1

Given,

The force applied on the puck, F=20 N

The mass of the puck, m=0.4 kg

The initial velocity of the puck, u=0 m/s

The final velocity of the puck, v=10 m/s

The time duration, t=0.2 s

The work done is given by the product of the force applied to the object and the distance to which the force was applied.

That is,

`W=F* d\text{ }\rightarrow\text{ (i)}`

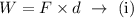
Where d is the distance traveled by the puck.

From the equation of motion,

`d=ut+(1)/(2)at^2`

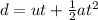
Where a is the accleration of the puck due to the applied force F.

But, the puck was at rest initially. Therefore,

`d=(1)/(2)at^2\text{ }\rightarrow\text{ (ii)}`

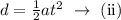
From Newton's second law of motion,

`\begin{gathered} F=ma \\ \Rightarrow a=(F)/(m)\text{ }\rightarrow\text{ (iii)} \end{gathered}`

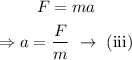
On substituting the equation (iii) in equation (ii),

`\begin{gathered} d=(1)/(2)*(F)/(m)* t^2 \\ =(Ft^2)/(2m)\text{ }\rightarrow(\text{iv)} \end{gathered}`

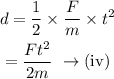
On substituting equation (iv) in equation (i),

`\begin{gathered} W=F*(Ft^2)/(2m) \\ =(F^2t^2)/(2m) \end{gathered}`

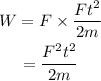
On substituting the known values in the above equation,

`\begin{gathered} W=(20^2*0.2^2)/(2*0.4) \\ =20\text{ J} \end{gathered}`

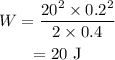
Therefore, the work done by the puck is 20 J