As you can see in the graph, we have two separated lines, for x-values less than -1 and for x values greater than 2, then we have to formulate two linear equations and join them into a piecewise function, like this:
The general form of a linear equation is y = mx + b, we can find the value of m with the following formula:

Where (x1, y1) and (x2, y2) are two points of the line.
• For the first line, when x < -1:
By taking the points (-1, -4) and (-3, 0), we get:
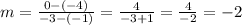
Then, the slope "m" of this line equals -2, we can find the value of b by replacing the value of m that we found into the formula of the line and replacing the x and y-values of one of the point of the line, like this:
By taking the point (-3, 0)
0 = -2×(-3) + b
0 = 6 + b
-6 = b
b = -6
Then, b equals -6, then the equation of the first line is:
y = -2x - 6
• For the second line, when x > 2
Similarly, for the second line, we can take the points (2, -3) and (4, -6), then we get:

now let's find the value of b with the point (2, -3)
-3 = -3/2×2 + b
-3 = -3 + b
0 = b
b = 0
b equals 0 and m equals -3/2, then the equation of this line is:
y = -3/2x
As mentioned, the first line is for the values of x that are less than 1 and the second one for ve x-values greater than 2, then we can write the following piecewise function: