We can divide the figure in two regular polygons:
then, the area and perimeter of the rectangle are the following:
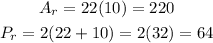
then, the area and perimeter of the semicircle are the following:
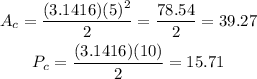
then, if we add the areas and the perimeters, we get:
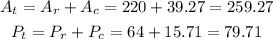
therefore, the area is 259.27 squared units and the perimeter is 79.71 units