Question

Calculate the mean, median, range, and midrange of thetrain ride times for the week.

Answer 1

The data set is given below as

`48,51,48,48,50`

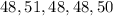
A) mean:

The mean is defined as the sum of values divided by the number of data set

`\begin{gathered} mean=\frac{totalsumofnumbers}{number\text{ of data set}} \\ \end{gathered}`

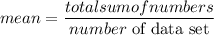
By substituting the values, we will have

`\begin{gathered} mean=\frac{totalsumofnumbers}{number\text{ofdataset}} \\ mean=(48+51+48+48+50)/(5) \\ mean=(245)/(5) \\ mean=49 \end{gathered}`

Hence,

The mean = 49

B) Median:

The median of a set of numbers is the middle number in the set (after the numbers have been arranged from least to greatest) -- or, if there are an even number of data, the median is the average of the middle two numbers.

By rearranging the data set, we will have

`\begin{gathered} 48,48,48,50,51 \\ The\text{ number in the middle is =48} \end{gathered}`

Hence,

The median = 48

C) Range:

The range is the difference between the highest and lowest values in a set of numbers. To find it, subtract the lowest number in the distribution from the highest.

`\begin{gathered} Range=highest\text{ number - lowest number} \\ highest\text{ number=51} \\ lowest\text{ number = 48} \\ range=51-48 \\ range=3 \end{gathered}`

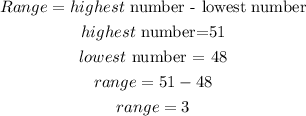
Hence,

The range = 3

D) Mid range:

The midrange of the data set is simply the value between the biggest value and the lowest value. In order to find the midrange of the data set the value is then divided by 2 after summing the lowest value present in the data set with the highest value present in the data set.

`\begin{gathered} midrange=(highestvalue+lowestvalue)/(2) \\ mid-range=(51+48)/(2) \\ mid-range=(99)/(2) \\ mid-range=49.5 \end{gathered}`

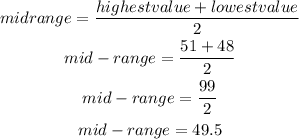
Hence,

The mid-range = 49.5

Therefore,

mean 49; median 48; range 3; midrange 49.5

The third OPTION is the right answer