Let w be the number of pounds of walnuts . Then, we can write
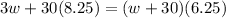
because the mixture (w+30) will cost $6.25 per pound. This equation can be written as
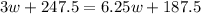
then, by moving 187.5 to the left hand side and 3w to the right hand side, we get
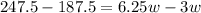
which gives
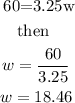
this means that we must mix 18.46 pounds of walnuts with 30 pounds of almonds which will costs $6.50 per pound