Question

Round to the nearest integer as needed and look at photo for accurate description

Answer 1

We will have to use the Law of Sines, which states that:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

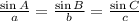
Procedure:

0. We have to remember that the sum of the interior angles of a right triangle adds up to 180°. Then:

`A+B+C=180`

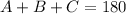
As we are given two angles, B and C, we can isolate for A:

`A=180-B-C`

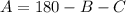
Replacing the values we get:

`A=180-42-100`
`A=38`

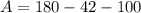
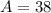
2. Now that we have the three angles, we can use the Law of Sines to get the sides:

`(\sin B)/(b)=(\sin C)/(c)`

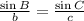
Isolating for c:

`c=(\sin C)/((\sin B)/(b))`

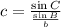
Replacing the values:

`c=(\sin 100)/((\sin 42)/(165))`
`c\approx243`

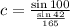
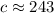
3. Finally, getting a also using the Law of Sines:

`a=(\sin A)/((\sin B)/(b))`

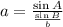
Replacing the values:

`a=(\sin 38)/((\sin 42)/(165))`
`a\approx152`

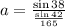
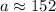
Answer: A.

• A = 38°

,

• a = 152m

,

• c = 243m