Question

How does the question gets i's and how to solve

Answer 1

`P(x)=x^3-3x^2+9x+13`

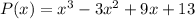
Applying the rational root theorem, the possible roots are:

`\pm\frac{\text{factors of the constantant term}}{\text{factors of the leading coefficient}}=(13,1)/(1)=\pm13,\pm1`

Evaluating P(x) with x = -1, we get:

`\begin{gathered} P(-1)=(-1)^3-3(-1)^2+9(-1)+13 \\ P(-1)=-1^{}-3-9+13 \\ P\mleft(-1\mright)=0 \end{gathered}`

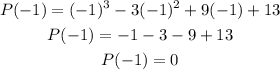
Then, (x + 1) is a factor of P(x). Dividing P(x) by (x+1) with the help of Ruffini's rule, we get:

This means that:

`\begin{gathered} (x^3-3x^2+9x+13)/(x+1)=x^2-4x+13 \\ x^3-3x^2+9x+13=(x^2-4x+13)(x+1) \end{gathered}`

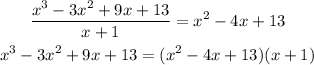
Now, we need to find the roots of:

`x^2-4x+13`

Using the quadratic formula with a = 1, b = -4, and c = 13, we get:

`\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{4\pm\sqrt[]{(-4)^2-4\cdot1\cdot13}}{2\cdot1} \\ x_(1,2)=\frac{4\pm\sqrt[]{-36}}{2} \\ x_1=(4+6i)/(2)=2+3i \\ x_2=(4-6i)/(2)=2-3i \end{gathered}`

In conclusion, the roots of P(x) are x = -1, 2+3i, 2-3i. And the x-intercept is x = -1 (the other roots are imaginary).