Since all the sides of the triangle are known, it is better to use Heron's formula for finding the area.
Consider the sides of the triangle as,

Solve for the semi-perimeter (s) as,
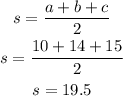
Then according to the Heron's Formula, the area (A) of the triangle is given by,
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
Substitute the values and simplify,
![\begin{gathered} A=\sqrt[]{19.5(19.5-10)(19.5-14)(19.5-15)} \\ A=\sqrt[]{19.5*9.5*5.5*4.5} \\ A=\sqrt[]{4584.9375} \\ A\approx67.7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/gyxtoeh0qw9hs2w1gsq9blzzqed1szijcd.png)
Thus, the area of the given triangle is 67.7 sq. km approximately.