Given
sides 17 ft, 14 ft, and 20 ft.
Recall that given three sides of a triangle, we can calculate the area using Heron's Formula which states that
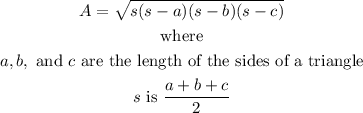
Solve for s first and we get
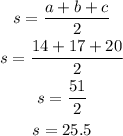
Next, use Heron's formula and we have
![\begin{gathered} A=√(s(s-a)(s-b)(s-c)) \\ A=√(25.5(25.5-14)(25.5-17)(25.5-20)) \\ A=\sqrt{25.5\cdot11.5\operatorname{\cdot}8.5\operatorname{\cdot}5.5} \\ A=√(13709.4375) \\ A=117.0873 \end{gathered}]()
Rounding our final answer to the nearest tenth, the area of the given triangle is 117.1 square feet.